于2022年底问世的ChatGPT,震撼了互联网。不由得使人联想起2016年初的AlphaGo,挑战人类顶级围棋大师李世石的故事。我在2017年出版的一本概率科普书中【1】,对当年人工智能的状况稍有描述,那算是AI的第二次革命,深度机器学习和自然语言处理(NLP)刚起步。没想到短短几年过去,第三次AI浪潮滚滚而来,基本搞定了自然语言的理解和生成难题,以 ChatGPT 发布为里程碑,开辟了人机自然交流的新纪元。

图1:OpenAI发布ChatGPT
人工智能(AI)的想法由来已久,英国数学家艾伦·图灵,不仅仅是计算机之父,也设计了著名的图灵试验,开启了人工智能的大门。如今,人工智能的应用已渗入到我们的日常生活中。它的成功崛起,来源于计算机的飞速发展、云计算的兴起、大数据时代的来临,等等。其中,与大数据有关的数学基础主要是概率论。因此,此文就聊聊ChatGPT与概率相关的一个方面,更具体来说,是与几百年前的一个人名有关:贝叶斯。
● ● ●
概率论和贝叶斯
针对概率论,有法国牛顿之称的拉普拉斯(1749年-1827年)曾说:
“这门源自赌博机运之科学,必将成为人类知识中最重要的一部分,生活中大多数问题,都将只是概率的问题。”
两百多年之后的当今文明社会,证实了拉普拉斯的预言。这个世界充满了不确定性,处处是概率,万物皆随机。无需抽象定义,概率论的基本直观概念早已渗透到人们的工作和生活当中,小到人人都可以买到的彩票,大到星辰宇宙,复杂到计算机和人工智能,都与概率密切相关。
那么,贝叶斯又是谁呢?
托马斯·贝叶斯(Thomas Bayes,1701年-1761年),是18世纪的一位英国数学家、统计学家,他曾经是个牧师。不过他“生前籍籍无名,死后众人崇拜”,在当代科技界“红”了起来,原因归结于以他命名的著名的贝叶斯定理。这个定理不仅在历史上促成了贝叶斯学派的发展,现在又被广泛应用于与人工智能密切相关的机器学习中【2】。
贝叶斯做了些什么?当年,他研究一个“白球黑球”的概率问题。概率问题可以正向计算,也能反推回去。例如,盒子里有10个球,黑白两种颜色。如果我们知道10个球中5白5黑,那么,如果我问你,从中随机取出一个球,这个球是黑球的概率是多大?问题不难回答,当然是50%!如果10个球是6白4黑呢?取出一个球为黑的概率应该是40%。再考虑复杂一点的情形:如果10个球中2白8黑,现在随机取2个球,得到1黑1白的概率是多少呢?10个球取出2个的可能性总数为10*9=90种,1黑1白的情况有16种,所求概率为16/90,约等于17.5%。因此,只需进行一些简单的排列组合运算,我们可以在10个球的各种分布情形下,计算取出n个球,其中m个是黑球的概率。这些都是正向计算概率的例子。
不过,当年的贝叶斯更感兴趣的是反过来的“逆概率问题”:假设我们预先并不知道盒子里黑球白球数目的比例,只知道总共是10个球,那么,比如说,我随机地拿出3个球,发现是2黑1白。逆概率问题则是要从这个试验样本(2黑1白),猜测盒子里白球黑球的比例。
也可以从最简单的抛硬币试验来说明“逆概率”问题。假设我们不知道硬币是不是两面公平的,也就是说,不了解这枚硬币的物理偏向性,这时候,得到正面的概率p不一定等于50%。那么,逆概率问题便是企图从某个(或数个)试验样本来猜测p的数值。
为了解决逆概率问题,贝叶斯在他的论文中提供了一种方法,即贝叶斯定理:
P(A|B) = (P(B|A) * P(A))/ P(B) (1)
这儿,A、B是两个随机事件,P(A)是A发生的概率;P(B)是B发生的概率。P(A|B)、P(B|A),称为条件概率:P(A|B)是在B发生的情况(条件)下A发生的概率;P(B|A)是在A发生的情况下B发生的概率。
应用贝叶斯定理的例子
可以从两个角度来解读贝叶斯定理:一是“表述了两个随机变量A和B的相互影响”;二是“如何修正先验概率而得到后验概率”,以下分别举例予以说明。
首先,初略地说,贝叶斯定理(1)涉及了两个随机变量A和B,表示两个条件概率P(A|B) 和P(B|A)之间的关系。
例1:某小城一月份治安不太好,30天内发生入室抢劫案6起。警察局有一个警报器,有事发生时便会拉响,包括火灾、暴风雨等天灾,及偷盗、强奸一类的人祸。一月份时,警报器每天都响。并且,从过去的经验,如果有居民遭入室抢劫时,警报器响的概率是0.85。现在人们又听到了警报声,那么,这次响声代表入室抢劫的概率是多少呢?
分析一下这个问题。A: 入室抢劫;B: 拉警报。然后,我们已知(一月份):
入室抢劫的概率P(A) = 6/30 = 0.2;拉警报的概率P(B) = 30/30 = 1;P(B|A) = 入室抢劫时拉警报的概率 = 0.85。
所以,根据公式(1),代入已知的3个概率,计算得到 P(A|B) = (0.85*0.2/1)= 0.17。
也就是说,这次“警报响的原因是有人入室抢劫”的概率是百分之十七。
下面举例说明如何用贝叶斯定理,从“先验概率”计算“后验概率”。首先将(1)改写为如下样子:
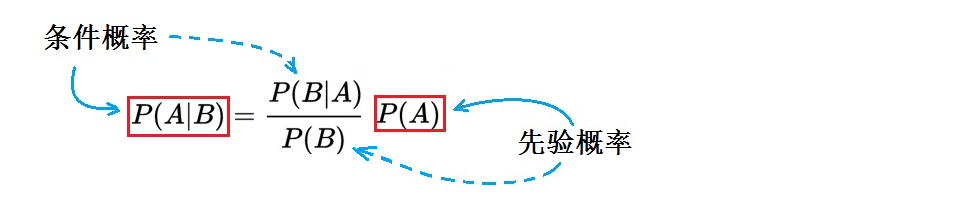
(2)
用一句话来概括(2),它说的是:利用B发生带来的新信息,可以修改当B未发生时A的“先验概率”P(A),从而得到B发生(或存在)时,A的“后验概率”,即P(A|B)。
首先用美国心理学家,2002年诺贝尔经济奖得主丹尼尔·卡尼曼举的一个例子简单说明。
例2:某城市有两种颜色(蓝绿)的出租车:蓝车和绿车的比率是15:85。某日某辆出租车夜间肇事后逃逸,但当时正好有一位目击证人,这位目击者认定肇事的出租车是蓝色的。但是,他“目击的可信度”如何呢?公安人员经过在相同环境下对该目击者进行“蓝绿”测试而得到:80%的情况下识别正确,20%的情况不正确,问题是计算肇事之车是蓝色的几率。
假设A=车为蓝色、B=目击蓝色。首先我们考虑蓝绿出租车的基本比例(15: 85)。也就是说,在没有目击证人的情况下,肇事之车是蓝色的几率为15%,这是“A=蓝车肇事”的先验概率P(A)= 15%。
现在,有了一位目击者,便改变了事件A出现的概率。目击者看到车是“蓝”色的。不过,他的目击能力也要打折扣,只有80%的准确率,即也是一个随机事件(记为B)。我们的问题是要求出在有该目击证人“看到蓝车”的条件下肇事车“真正是蓝色”的概率,即条件概率P(A|B)。后者应该大于先验概率15%,因为目击者看到“蓝车”。如何修正先验概率?需要计算P(B|A)和P(B)。
因为P(B|A)是在“车为蓝色”的条件下“目击蓝色”的概率,即P(B|A) =80%。概率P(B)的计算麻烦一点。P(B)指的是目击证人看到一辆车为蓝色的概率,应该等于两种情况的概率相加:一种是车为蓝色,辨认也正确;另一种是车为绿,错看成蓝。
